In a previous post I showed you how to use my open source python backtesting package, pysystemtrade, to estimate forecast weights and instrument weights. At the time I hadn't included code to calculate costs. Now that has been remedied I thought I should also write some code to demonstrate the different ways you can optimise in the presence of costs.
You can see what else has been included in pysystemtrade since you last checked, here. If you're not a fan of pysystemtrade, don't worry, you'll probably find the discussion interesting although you'll then have to work out how to implement it yourself.
Naturally your understanding and enjoyment of this post will be enhanced if you've read chapter 12 of my book, though non readers who have followed my blog posts on the subject of optimisation should also be fine.
This post has been modified to reflect the changes made in version 0.10.0
In this first part of the post I'll discuss in general terms the different ways of dealing with costs. Then I'll show you how to do this in python, with some pretty pictures.
Ignore costs - use gross returns
I'm assuming here you've calculated your costs properly and not been overly optimistic.
Take for example my own trading system. It backtests at something like a 20% average return before costs. As it happens I came in just over that last year. But I expect just over two thirds of my annual returns to be somewhere between -5% and +45% (this is a simple confidence interval given a standard deviation of 25%).
Costs however are a different matter. My costs for last year came in at 1.39% versus a backtested 1.5%. I am pretty confident they will be between 1% and 2% most years I trade. Costs of 1.5% don't affect optimisation much, but if your predicted costs were 15% versus a 20% gross return, then it's important you bear in mind your costs have perhaps a 70% chance of being between 14% and 16%, and your gross returns between -5% and 45%. That's a system I personally wouldn't trade.
The next few alternatives involve various ways of dealing with this issue.
This is probably the most extreme solution - throw away any information about gross returns and optimise purely on cost data. Expensive assets will get a lower weight than cheap ones.
(Note this should be done in a way that preserves the covariance structure of gross returns; since we still want more diversifying assets to be upweighted. It's also good for optimisation to avoid negative returns. I apply a drag to the returns such that the asset's Sharpe Ratios are equal to the cost difference plus a reasonable average Sharpe)
I quite like this idea. I think it's particularly appealing in the case of allocating instrument weights in a portfolio of trading systems, each trading one instrument. There is little reason to think that one instrument will do better than another.
Nevertheless I can understand why some people might find this a little extreme, and I probably wouldn't use it for allocating forecast weights to trading rule variations. This is particularly the case if you've been following by general advice not to fit trading models in the "design" phase, which means an optimiser needs to be able to underweight a poor model.
This is a slightly more sophisticated method and one that Thomas Bayes FRS would be more comfortable with.
In table 12 (chapter 4, p.86 print edition) of my book I explain how you can adjust portfolio weights if you know with certainty what the Sharpe ratio difference is between the distribution of returns of the assets in our portfolio (notice this is not as strong as saying we can predict the actual returns). Since we have a pretty good idea what costs are likely to be (so I'm happy to say we can predict their distribution with something close to certainty) it's valid to use the following approach:
I'm a big fan of pooling information across different instruments.
This section applies only to calculating forecast weights; you can't pool data across instruments to work out instrument weights.
It's rare to have enough data for any one instrument to be able to say with any statistical significance that this trading rule is better than the other one. We often need decades of data to make that decision. Decades of data just aren't available except for a few select markets. But if you have 30 instruments with 10 years of data each, then that's three centuries worth.
Once we start thinking about pooling with costs however there are a few different ways of doing it.
This is the simplest solution; but if our instruments have radically different costs it may prove fatal. In a field of mostly cheap instruments we'd plump for a high return, high turnover, trading rule. When applied to a costly instrument that would be a guaranteed money loser.
This is the "throw our toys out of the pram" solution to the point I raised above. Of course we lose all the benefits of pooling.
This is a nice compromise. The idea being once again that gross returns are relatively unpredictable (so let's get as much data as possible about them), whilst costs are easy to forecast on an instrument by instrument basis (so let's use them).
Notice that the calculation for cost comes in two parts - the cost "per turnover" (buy and sell) and the number of turnovers per year. So we can use some pooled information about costs (the average turnover of the trading rule), whilst using the relevant cost per turnover of an individual instrument.
I hopefully don't need to point out to the intelligent readers of my blog that using an instrument's own gross returns, but with pooled costs, is pretty silly.
This is an extract from a pysystemtrade YAML configuration file:
forecast_weight_estimate:
date_method: expanding ## other options: in_sample, rolling
rollyears: 20
frequency: "W" ## other options: D, M, Y
I'll focus on the weights for Eurostoxx (as it's the cheapest market in the chapter 15 set) and V2X (the most expensive one); although of course in this first example they'll be the same as I'm pooling net returns. Although I'm doing all my optimisation on a rolling out of sample basis I'll only be showing the final set of weights.
forecast_cost_estimates:
use_pooled_costs: True
forecast_weight_estimate:
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 0.0
pool_gross_returns: True
equalise_gross: False
# optimisation parameters remain the same
method: bootstrap
equalise_vols: True
monte_runs: 100
bootstrap_length: 50
equalise_SR: False
frequency: "W"
date_method: "expanding"
rollyears: 20
cleaning: True
These are the Eurostoxx weights; but they're the same for every market. As you can see the diversifying carry rule gets the most weight; for the variations of EWMAC it's close to equal weights.
For a cheap market like Eurostoxx applying it's own costs means that the fast EWMAC2_8 isn't downweighted by nearly as much as with pooled costs. There's also the fact that we haven't much data, which means the weights could be a bit unusual.
V2X is expensive, so there's a bit less weight on ewmac2. However again there's actually more than for the pooled data above; suggesting again that the small amount of data available is just giving us rather random weights.
These two graphs are far more sensible. There is about 30% in carry in both; with pretty much equal weighting for the cheaper Eurostoxx market, and a tilt towards the cheaper variations for pricey V2X.
For the rest of this post I'll be using this combination.
For cheap Eurostoxx costs don't seem to matter much and there's a spread to the more diversifying 'wings' driven by correlations. For V2X there is clearly a tilting away from the more expensive options, but it isn't dramatic.
I've used a factor of 3 here rather than 2 to make the picture more dramatic. The results show about half the weight for V2X in the most expensive variation compared to using a cost factor of 1. Still I have my reservations about what the right number to use is here.
apply_cost_weight: True
ceiling_cost_SR: 999.0
cost_multiplier: 0.0
pool_gross_returns: True
equalise_gross: False
This gives similar results to using a cost multiplier of 3.0 above.
apply_cost_weight: False
ceiling_cost_SR: 0.13
cost_multiplier: 1.0
pool_instruments: True
equalise_gross: False
forecast_cost_estimates:
use_pooled_costs: False
As you'll know from reading my book I like the idea of culling expensive trading rules. This leaves the optimiser with less to do. I really like the idea of applying cost weighting (versus say multiplying costs my some arbitrary figure); which means optimising on gross returns. Equalising the returns before costs seems a bit extreme to me; I'd still like the idea of really poor trading rules being downweighted, even if they are the cheap ones. Pooling gross returns but using instrument specific costs strikes me as the most logical route to take.
You can see what else has been included in pysystemtrade since you last checked, here. If you're not a fan of pysystemtrade, don't worry, you'll probably find the discussion interesting although you'll then have to work out how to implement it yourself.
Naturally your understanding and enjoyment of this post will be enhanced if you've read chapter 12 of my book, though non readers who have followed my blog posts on the subject of optimisation should also be fine.
This post has been modified to reflect the changes made in version 0.10.0
Costs, generally
In this first part of the post I'll discuss in general terms the different ways of dealing with costs. Then I'll show you how to do this in python, with some pretty pictures.
How to treat costs
Ignore costs - use gross returns
This is by far the simplest option. It's even okay to do it if the assets in your portfolio optimisation, whether they be trading rules or instruments, have the same costs. Of course if this isn't the case you'll end up overweighting anything that looks amazing pre-costs, but has very high costs to go with it.
Subtract costs from gross returns: use net returns
This is what most people would do without thinking; it's perhaps the "obvious" solution. However this skips over a fairly fundamental problem, which is this: We know costs with more certainty than we know expected gross returns.I'm assuming here you've calculated your costs properly and not been overly optimistic.
Take for example my own trading system. It backtests at something like a 20% average return before costs. As it happens I came in just over that last year. But I expect just over two thirds of my annual returns to be somewhere between -5% and +45% (this is a simple confidence interval given a standard deviation of 25%).
Costs however are a different matter. My costs for last year came in at 1.39% versus a backtested 1.5%. I am pretty confident they will be between 1% and 2% most years I trade. Costs of 1.5% don't affect optimisation much, but if your predicted costs were 15% versus a 20% gross return, then it's important you bear in mind your costs have perhaps a 70% chance of being between 14% and 16%, and your gross returns between -5% and 45%. That's a system I personally wouldn't trade.
The next few alternatives involve various ways of dealing with this issue.
Ignore gross returns, just use costs
This is probably the most extreme solution - throw away any information about gross returns and optimise purely on cost data. Expensive assets will get a lower weight than cheap ones.
(Note this should be done in a way that preserves the covariance structure of gross returns; since we still want more diversifying assets to be upweighted. It's also good for optimisation to avoid negative returns. I apply a drag to the returns such that the asset's Sharpe Ratios are equal to the cost difference plus a reasonable average Sharpe)
I quite like this idea. I think it's particularly appealing in the case of allocating instrument weights in a portfolio of trading systems, each trading one instrument. There is little reason to think that one instrument will do better than another.
Nevertheless I can understand why some people might find this a little extreme, and I probably wouldn't use it for allocating forecast weights to trading rule variations. This is particularly the case if you've been following by general advice not to fit trading models in the "design" phase, which means an optimiser needs to be able to underweight a poor model.
Subtract costs from gross returns, and multiply costs by a factor
This is a compromise where we use gross returns, but multiply our costs by a factor (>1) before calculating net costs. A common factor is 2, derived from the common saying "A bird in the hand is worth two in the bush", or in the language of Bayesian financial economics: "A bird which we have in our possession with 100% uncertainty has the same certainty equivalent value as two birds whose ownership and/or existence has a probability of X% (solve for X according to your own personal utility function)".
In other words 1% of extra costs is worth as much as 2% of extra gross returns. This has the advantage of being simple, although it's not obvious what the correct factor is. The correct factor will depend on the sampling distribution of the gross returns, and that's even without getting into the sticky world of uncertainty adjustment for personal utility functions.
Calculate weights using gross returns, and adjust subsequently for cost levels
 |
| I'm 97% sure this is Thomas Bayes. Ex-ante I was 100%, but the image is from Wikipedia after all. |
In table 12 (chapter 4, p.86 print edition) of my book I explain how you can adjust portfolio weights if you know with certainty what the Sharpe ratio difference is between the distribution of returns of the assets in our portfolio (notice this is not as strong as saying we can predict the actual returns). Since we have a pretty good idea what costs are likely to be (so I'm happy to say we can predict their distribution with something close to certainty) it's valid to use the following approach:
- Make a first stab at the portfolio weights using just gross returns. The optimiser (assuming you're using bootstrapping or shrinkage) will automatically incorporate the uncertainty of gross returns into it's work.
- Using the Sharpe Ratio differences of the costs of each asset adjust the weights.
This trick means we can pull in two types of data about which we have differing levels of statistical confidence. It's also simpler than the strictly correct alternative of bootstrapping some weights with only cost data, and then combining the weights derived from using gross returns with those from costs.
Apply a maximum cost threshold
In chapter 12 of my book I recommended that you do not use any trading system which sucked up more than 0.13 SR of costs a year. Although all the methods above will help to some extent, it's probably a good idea to entirely avoid allocating to any system which has excessive costs.
Different methods of pooling
This section applies only to calculating forecast weights; you can't pool data across instruments to work out instrument weights.
It's rare to have enough data for any one instrument to be able to say with any statistical significance that this trading rule is better than the other one. We often need decades of data to make that decision. Decades of data just aren't available except for a few select markets. But if you have 30 instruments with 10 years of data each, then that's three centuries worth.
Once we start thinking about pooling with costs however there are a few different ways of doing it.
Full pooling: Pool both gross returns and costs
This is the simplest solution; but if our instruments have radically different costs it may prove fatal. In a field of mostly cheap instruments we'd plump for a high return, high turnover, trading rule. When applied to a costly instrument that would be a guaranteed money loser.
Don't pool: Use each instruments own gross returns and costs
This is the "throw our toys out of the pram" solution to the point I raised above. Of course we lose all the benefits of pooling.
Half pooling: Use pooled gross returns, and an instrument's own costs
This is a nice compromise. The idea being once again that gross returns are relatively unpredictable (so let's get as much data as possible about them), whilst costs are easy to forecast on an instrument by instrument basis (so let's use them).
Notice that the calculation for cost comes in two parts - the cost "per turnover" (buy and sell) and the number of turnovers per year. So we can use some pooled information about costs (the average turnover of the trading rule), whilst using the relevant cost per turnover of an individual instrument.
Note
I hopefully don't need to point out to the intelligent readers of my blog that using an instrument's own gross returns, but with pooled costs, is pretty silly.
Costs in pysystemtrade
You can follow along here. Notice that I'm using the standard futures example from chapter 15 of my book, but we're using all the variations of the ewmac rule from 2_8 upwards to make things more exciting.
Key
This is an extract from a pysystemtrade YAML configuration file:
forecast_weight_estimate:
date_method: expanding ## other options: in_sample, rolling
rollyears: 20
frequency: "W" ## other options: D, M, Y
Forecast weights
Let's begin with setting forecast weights. I'll begin with the simplest possible behaviour which is:- applying no cost weighting adjustments
- applying no ceiling to costs before weights are zeroed
- A cost multiplier of 0.0 i.e. no costs used at all
- Pooling gross returns across instruments and also costs; same as pooling net returns
- Using gross returns without equalising them
I'll focus on the weights for Eurostoxx (as it's the cheapest market in the chapter 15 set) and V2X (the most expensive one); although of course in this first example they'll be the same as I'm pooling net returns. Although I'm doing all my optimisation on a rolling out of sample basis I'll only be showing the final set of weights.
forecast_cost_estimates:
use_pooled_costs: True
forecast_weight_estimate:
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 0.0
pool_gross_returns: True
equalise_gross: False
# optimisation parameters remain the same
method: bootstrap
equalise_vols: True
monte_runs: 100
bootstrap_length: 50
equalise_SR: False
frequency: "W"
date_method: "expanding"
rollyears: 20
cleaning: True
Subtract costs from gross returns: use net returns
forecast_cost_estimates:
use_pooled_costs: True
forecast_weight_estimate:
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0 ## note change
pool_gross_returns: True
equalise_gross: False
Again just the one set of weights here. There's a bit of a reallocation from expensive and fast trading rules towards slower ones, but not much.
use_pooled_costs: True
forecast_weight_estimate:
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0 ## note change
pool_gross_returns: True
equalise_gross: False
Don't pool: Use each instruments own gross returns and costs
forecast_cost_estimates:
use_pooled_costs: False
use_pooled_costs: False
forecast_weight_estimate:
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0
pool_gross_returns: False
equalise_gross: False
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0
pool_gross_returns: False
equalise_gross: False
 |
| EUROSTX (Cheap market) |
 |
| V2X (Expensive market) |
Half pooling: Use pooled gross returns, and an instrument's own costs
forecast_cost_estimates:
use_pooled_costs: False
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0
pool_gross_returns: True
equalise_gross: False
use_pooled_costs: False
use_pooled_turnover: True ## even when pooling I recommend doing this
forecast_weight_estimate:apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0
pool_gross_returns: True
equalise_gross: False
 |
| EUROSTOXX (Cheap) |
 |
| V2X (Expensive) |
These two graphs are far more sensible. There is about 30% in carry in both; with pretty much equal weighting for the cheaper Eurostoxx market, and a tilt towards the cheaper variations for pricey V2X.
For the rest of this post I'll be using this combination.
Ignore gross returns, just use costs
forecast_cost_estimates:
use_pooled_costs: False
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0
pool_gross_returns: True
equalise_gross: True
use_pooled_costs: False
use_pooled_turnover: True ## even when not pooling costs I recommend doing this
forecast_weight_estimate:apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 1.0
pool_gross_returns: True
equalise_gross: True
 |
| Eurostoxx (cheap) |
 |
| V2X (expensive) |
Subtract costs from gross returns after multiply costs by a factor>1
forecast_cost_estimates:
use_pooled_costs: False
use_pooled_costs: False
use_pooled_turnover: True ## even when pooling I recommend doing this
forecast_weight_estimate:
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 3.0
pool_gross_returns: True
equalise_gross: False
apply_cost_weight: False
ceiling_cost_SR: 999.0
cost_multiplier: 3.0
pool_gross_returns: True
equalise_gross: False
 |
| Eurostoxx (Expensive) |
 |
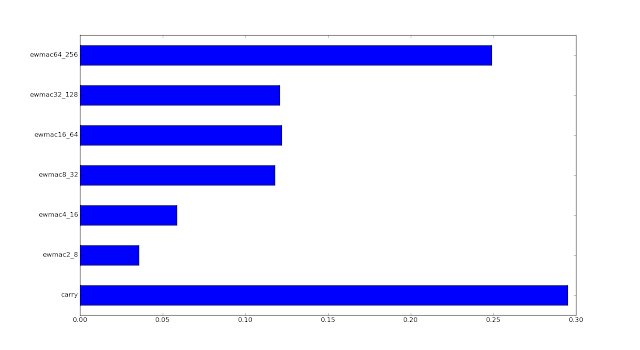| V2X (Cheap) |
Calculate weights using gross returns, and adjust subsequently for cost levels
forecast_cost_estimates:
use_pooled_costs: False
use_pooled_turnover: True ## even when pooling I recommend doing this
forecast_weight_estimate:apply_cost_weight: True
ceiling_cost_SR: 999.0
cost_multiplier: 0.0
pool_gross_returns: True
equalise_gross: False
 |
| EUROSTOXX (Cheap) |
 |
| V2X (Expensive) |
Apply a maximum cost threshold
forecast_cost_estimates:
use_pooled_costs: False
use_pooled_turnover: True ## even when pooling I recommend doing this
forecast_weight_estimate:apply_cost_weight: False
ceiling_cost_SR: 0.13
cost_multiplier: 1.0
pool_instruments: True
equalise_gross: False
 |
| EUROSTOXX (Cheap) |
 |
| V2X (Expensive) |
Really giving any allocation to ewmac2_8 has been kind of crazy because it is a rather expensive beast to trade. The V2X weighting is even more extreme removing all but the 3 slowest EWMAC variations. It's for this reason that chapter 15 of my book uses only these three rules plus carry.
My favourite setup
forecast_cost_estimates:
use_pooled_costs: False
use_pooled_turnover: True ## even when pooling I recommend doing this
forecast_weight_estimate:
apply_cost_weight: True
ceiling_cost_SR: 0.13
ceiling_cost_SR: 0.13
cost_multiplier: 0.0
pool_gross_returns: True
equalise_gross: False
As you'll know from reading my book I like the idea of culling expensive trading rules. This leaves the optimiser with less to do. I really like the idea of applying cost weighting (versus say multiplying costs my some arbitrary figure); which means optimising on gross returns. Equalising the returns before costs seems a bit extreme to me; I'd still like the idea of really poor trading rules being downweighted, even if they are the cheap ones. Pooling gross returns but using instrument specific costs strikes me as the most logical route to take.
 |
| Eurostoxx (cheap) |
 |
| V2X (expensive) |
A note about other optimisation methods
The other three methods in the package are shrinkage and one shot optimisation (just a standard mean variance). I don't recommend using the latter for reasons which I've mentioned many, many times before. However if you're using shrinkage be careful; the shrinkage of net return Sharpe Ratios will cancel out the effect of costs. So again I'd suggest using a cost ceiling, setting the cost multiplier to zero, then applying a cost weighting adjustment; the same setup as for bootstrapping.
forecast_cost_estimates: use_pooled_costs: False use_pooled_turnover: True ## even when pooling I recommend doing thisforecast_weight_estimate:
method: shrinkage equalise_SR: False
ann_target_SR: 0.5
equalise_vols: True
shrinkage_SR: 0.90
shrinkage_corr: 0.50
apply_cost_weight: True
ceiling_cost_SR: 0.13
cost_multiplier: 0.0
pool_instruments: True
pool_costs: False
equalise_gross: False
forecast_cost_estimates:
use_pooled_costs: False
use_pooled_turnover: True ## even when pooling I recommend doing this
forecast_weight_estimate: method: shrinkage
equalise_SR: Falseann_target_SR: 0.5
equalise_vols: True
shrinkage_SR: 0.90
shrinkage_corr: 0.50
apply_cost_weight: True
ceiling_cost_SR: 0.13
cost_multiplier: 0.0
pool_instruments: True
pool_costs: False
equalise_gross: False
ceiling_cost_SR: 0.13
cost_multiplier: 0.0
pool_instruments: True
pool_costs: False
equalise_gross: False
The Eurostoxx weights are very similar to those with bootstrapping. For V2X shrinkage ends up putting about 60% in carry with the rest split between the 3 slowest ewmac variations. This is more a property of the shrinkage method, rather than the costs. Perhaps the shrinkage isn't compensating enough for the uncertainty in the correlation matrix, which the bootstrapping does.
If you don't want to pool gross returns you might want to consider a higher shrinkage factor as there is less data (one of the reasons I don't like shrinkage is the fact the optimum shrinkage varies depending on the use case).
There's a final method equal_weight which will give equal weights (duh). However it can be used in combination with ceiling_cost_SR and apply_cost_weights.Instrument weights
In my book I actually suggested that ignoring costs for instrument trading subsystems is a perfectly valid thing to do. In fact I'd be pretty happy to equalise Sharpe ratios in the final optimisation and just let correlations do the talking.
Note that with instrument weights we also don't have the benefit of pooling. Also by using a ceiling on costs for trading rule variations it's unlikely that any instrument subsystem will end up breaking that ceiling.
Just for fun I ran an instrument weight optimisation with the same cost parameters as I suggested for forecasts. There is a smaller allocation to V2X and Eurostoxx; but that's probably because they are fairly highly correlated. One is the cheapest and the other the most expensive market, so the different weights are not driven by costs!
Key points from this post:
Happy optimising.
Portfolio optimization
pysystemtrade
Systematic_Trading_Book
Systems building
Uncertainty
Note that with instrument weights we also don't have the benefit of pooling. Also by using a ceiling on costs for trading rule variations it's unlikely that any instrument subsystem will end up breaking that ceiling.
 |
| Instrument weights |
Summary
Key points from this post:
- Pooling gross returns data across instruments - good thing
- Using instrument specific costs - important
- Filtering out trading rules that are too expensive - very very important
- Using a post optimisation cost weighting - nice, but not a dealbreaker
- Using costs when estimating instrument weights - less important
Happy optimising.